모델 평가 지표 정리
고려대학교 산업공학과 김태연님의 모델 평가 지표 정리 세미나(https://www.youtube.com/watch?v=4ZOH9DRbN0k)를 보고 정리 하였습니다.
Intro
평가지표에 대한 내용을 알아 보기전에 이 모델 평가 지표를 사용하는 기계학습(Machine learning)에 대해서 먼저 알아보겠습니다.
Machine learning
기계학습이란 컴퓨터가 학습할 수 있도록 하는 알고리즘과 기술을 개발하는 분야 입니다.
예를 들어 아래와 같이 label이 없는 비지도 학습을 통해 패턴이 비슷한 것들 끼리 컴퓨터의 계산과정을 통해 분류하는 것입니다.

이 Machine learning에 대한 과정은 5가지로 나눌 수 있습니다.
- 데이터 수집 (Data collection): 목적에 적합한 데이터를 모으는 작업
- 데이터 전처리 (Data preprocessing): 수집된 데이터 중 결측치, 이상치를 정제하는 작업등을 통해 분석에 적합한 형태로 바꿔주는 과정
- 모델 학습 (Model training): 전처리 된 데이터를 통해 올바른 예측이 가능하도록 규칙을 찾는 과정
- 모델 평가 (Model evaluation): 학습이 이루어진 모델이 어느 수준의 성능으로 예측이 가능한지 파악하는 과정
- 모델 최종 선택 및 적용 (Model selection): 모델 선택 및 적용: 모델 평가 과정에서 가장 우수한 성느의 모델을 선택하고, 해당 모델을 활용하여 적용하는 과

올바른 모델을 태스크에 적용하기 위해 적합한 평가지표 선택이 중요하기 때문에 평가지표를 선택하는 것은 매우 중요합니다. 다음으로는 어떤 모델에서 어떤 평가지표를 사용하는지에 대한 내용입니다.
회귀 모델 평가(Regression model evaluation)
우선 회귀 모델이란 여러가지 데이터들(독립 변수 X)을 통해 목표(종속 변수)를 예측하는 모델입니다.

다음은 회귀 모델을 평가하는 지표 6가지에 대해서 알아보겠습니다.
Mean Absolute Error(MAE)

MAE는 다음과 같은 특징이 있습니다.
- 실제 값과 모델이 예측한 값 차이의 절대값들의 평균값
- 절대값을 통해 양의 에러와 음의 에러가 상쇄되는 효과 제거
- 실제 데이터와의 통일된 단위로 분석이 직관적이라는 장점
- 실제 값과 비교해 예측 값이 보다 크거나 작은지 파악의 어려움
예시는 아래와 같습니다.

Mean Squared Error(MSE)

MSE는 아래와 같은 특징이 있습니다.
- 실제 갑소가 모델이 예측한 값 차이를 제곱한 값들의 평균 값
- 실제 값과 예측 값의 차이(=에러)를 제곱하여서 1미만의 에러는 보다 작아지며, 1이상의 에러는 보다 커지게 하여서 값의 왜곡 발생으로 이상치에 보다 민감함
- 실제 데이터와의 단위가 통일 되어 있지 않아 추가적인 해석이 필요하며, 실제 값과 비교해 예측 값이 보다 크거나 작은지 파악의 어려움
예시는 아래와 같습니다.

Root Mean Squared Error(RMSE)

RMSE는 아래와 같은 특징이 있습니다.
- MSE에 루트를 씌운 값
- MSE에서 에러의 제곱을 통한 왜곡 발생을 방지하며 실제 오류 값들 보다 더욱 커지는 특성을 방지
- 실제 데이터와의 단위 통일로 해석이 용이함
- 실제 값과 비교해 예측 값이 보다 크거나 작은지 파악의 어려움
예시는 아래와 같습니다.

Root Mean Squared Log Error(RMSLE)

RMSLE는 아래와 같은 특징이 있습니다.
- RMSE에 로그를 적용해준 지표
- 직관적이지 않은 값으로 에러를 통한 해석에는 어려움
- RMSE에서 값의 절대적 크기에 영향을 많이 받는 단점을 해결하기 위한 상대적인 에러
- 실제 값보다 작게 예측을 진행하는 경우 더욱 큰 패널티를 부여하는 지표
예시는 아래와 같습니다.


Mean Absolute Percentage Error(MAPE)

MAPE는 아래와 같은 특징이 있습니다.
- MAE를 비율로 변환하여 표현한 값
- 크기 의존적인 에러의 문제점인 단위의 차이가 크게 나타나는 경우 해석이 어려웠던 문제점을 해결
- 실제 값에 0이 포함된 경우에는 사용이 불가
예시는 아래와 같습니다.

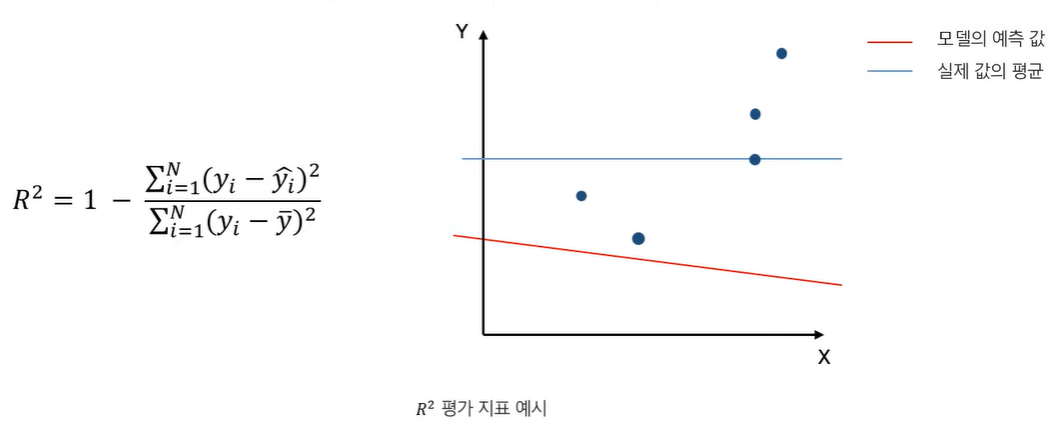
결정계수(R^2)

결정계수는 아래와 같은 특징이 있습니다.
- 데이터의 분산을 기반으로 한 평가 지표로 결정 계수라고 불림
- 데이터의 크기에 따라 영향을 받지 않는 평가지표로, 다른 지표들과는 큰 값을 가질수록 좋은 성능
- 모델이 예측을 모두 평균으로 하는 것보다 큰 오차를 보인다면 음(-)의 값을 보임
예시는 아래와 같습니다.

다음으로는 분류모델의 평가지표에 대한 내용입니다.
Classification model evaluation
분류모델은 주어진 데이터들이 속하는 클래스로 나누는 모델 입니다.

분류 모델의 평가지표를 알기 위해서 혼동행렬(Confusion matrix)에 대한 내용을 알고 있다면 수월합니다. 다음은 Confusion matrix에 대한 내용입니다.
혼동 행렬(Confusion matrix)

- 실제 정답과 모델의 예측 결과를 행렬의 형태로 표기한 것
- True / False: 실제 정답과 모델의 예측 결과가 동일한지 / 동일하지 않은지를 표현
- Positive / Negative: 모델의 예측 결과에 대한 표현
다음은 혼동행렬과 관련된 분류 모델을 평가하는 지표 4가지에 대해서 알아보겠습니다.
정확도(Accuracy)

- 전체 데이터 중 올바르게 분류가 이루어진 데이터의 비율
- 해석에 있어서 가장 직관적인 평가 지표지만, 데이터 사이의 불균형 문제가 있을 경우 적절하지 못한 평가지표
예시는 다음과 같습니다.

정밀도 (Precision)

- 모델이 positive로 분류를 진행한 데이터 중에서, 실제 결과도 positive인 데이터의 비율
- 모델이 positive로 예측하였지만 실제 결과가 negative일 때 큰 문제가 생기는 상황에서 사용되는 지표
예시는 다음과 같습니다.

재현율 (Recall)

- 실제 결과가 positive인 데이터 중에서, 모델이 positive로 분류한 데이터의 비율
- 실제 값이 positive일 때, 모델의 예측 값도 positive인 경우가 중요한 상황일 때 사용되는 지표
예시는 다음과 같습니다.

F{B} - score
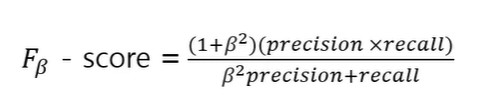
- 정밀도와 재현율의 trade-off 관계로 두 값을 동시에 높게 하는 것이 어려움
- 정밀도와 재현율의 가중조화평균을 활용하여 정밀도와 재현율의 값을 하나의 값으로 표현한 지표
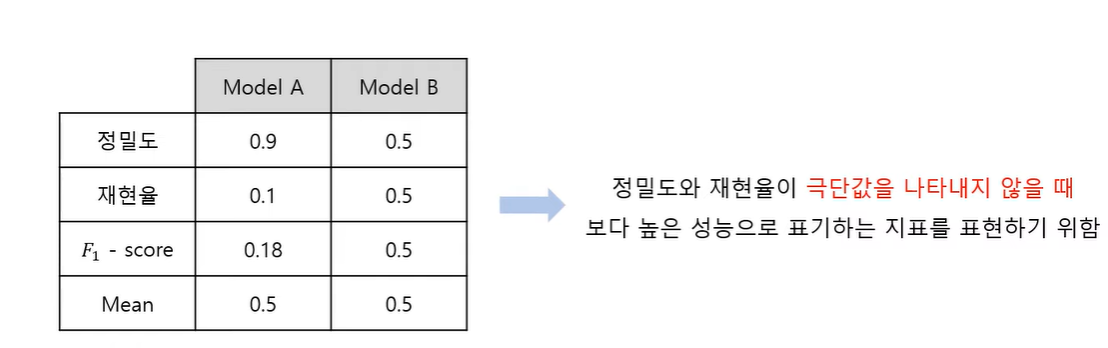
- 정밀도에 주어진 가중치를 B라 하며, B=1인 경우를 F1 - score를 의미
예시는 다음과 같습니다.

임계값(Threshold)
- 특정 클래스로 분류하기 위한 기준치로 이진 분류에서는 기본적으로 0.5로 설정
- 임계값 설정에 따라서 정밀도와 재현율의 값이 달라지는데, 정밀도와 재현율을 균형 있게 예측하는 적절한 임계값을 설정

ROC curve & AUC

- ROC curve : X축을 Fall-out 지표, Y축을 Recall 지표로 하는 그래프로 표현하는 방식
- Fall-out: 실제 결과가 negative인 데이터 중에서, 모델이 positive로 분류한 데이터의 비율
- AUC: ROC curve를 수치화한 값으로, ROC curve의 면적을 의미